Идеал хий, идеал хийн төлөвийн тэгшитгэл, түүний температур ба даралт, эзэлхүүн… Физикийн харгалзах хэсэгт ашигласан параметр, тодорхойлолтуудын жагсаалтыг нэлээд удаан үргэлжлүүлэх боломжтой. Өнөөдөр бид зөвхөн энэ сэдвээр ярилцах болно.
Молекулын физикт юу гэж үздэг вэ?

Энэ хэсэгт авч үзэх гол объект бол хамгийн тохиромжтой хий юм. Хүрээлэн буй орчны хэвийн нөхцлийг харгалзан хийн төлөв байдлын хамгийн тохиромжтой тэгшитгэлийг олж авсан бөгөөд бид энэ талаар бага зэрэг дараа ярих болно. Одоо энэ "асуудал"-д холоос хандъя.
Бидэнд хийн масс байна гэж бодъё. Түүний төлөвийг термодинамик шинж чанартай гурван параметрийг ашиглан тодорхойлж болно. Эдгээр нь мэдээжийн хэрэг даралт, эзэлхүүн, температур юм. Энэ тохиолдолд системийн төлөв байдлын тэгшитгэл нь холбогдох параметрүүдийн хоорондын хамаарлын томъёо байх болно. Энэ нь дараах байдалтай харагдана: F (p, V, T)=0.
Энд бид анх удаагаа хамгийн тохиромжтой зүйл гарч ирэхэд аажмаар ойртож байна.хий. Молекулуудын хоорондын харилцан үйлчлэл бага байдаг хий гэж нэрлэдэг. Ерөнхийдөө энэ нь байгальд байдаггүй. Гэсэн хэдий ч маш ховордсон хий нь түүнд ойрхон байдаг. Хэвийн нөхцөлд байгаа азот, хүчилтөрөгч, агаар нь хамгийн тохиромжтой байдлаас бага зэрэг ялгаатай. Идеал хийн төлөвийн тэгшитгэлийг бичихийн тулд хийн нэгдсэн хуулийг ашиглаж болно. Бид дараахыг авна: pV/T=const.
Холбогдох ухагдахуун №1: Авогадрогийн хууль
Хэрэв бид ямар ч санамсаргүй хийн ижил тооны моль авч, температур, даралт зэрэг ижил нөхцөлд хийвэл хийнүүд ижил эзэлхүүнийг эзэлнэ гэж тэр хэлж чадна. Тодруулбал, туршилтыг хэвийн нөхцөлд хийсэн. Энэ нь температур 273.15 Кельвин, даралт нь нэг атмосфер (760 миллиметр мөнгөн ус буюу 101325 Паскаль) байсан гэсэн үг юм. Эдгээр параметрүүдээр хий нь 22.4 литр эзэлхүүнтэй байв. Тиймээс аливаа хийн нэг моль хувьд тоон үзүүлэлтүүдийн харьцаа тогтмол байх болно гэж хэлж болно. Тийм ч учраас энэ дүрсийг R үсгээр тэмдэглэж, бүх нийтийн хийн тогтмол гэж нэрлэхээр шийдсэн. Энэ нь 8.31-тэй тэнцэнэ. Нэгж нь Ж/мольК.
Хамгийн тохиромжтой бензин. Төлөвийн хамгийн тохиромжтой хийн тэгшитгэл ба түүний зохицуулалт
Томьёог дахин бичиж үзье. Үүнийг хийхийн тулд бид үүнийг дараах хэлбэрээр бичнэ: pV=RT. Дараа нь бид энгийн үйлдэл хийж, тэгшитгэлийн хоёр талыг дурын тооны мольоор үржүүлнэ. Бид pVu=uRT авдаг. Молийн эзэлхүүний бүтээгдэхүүн ба гэдгийг харгалзан үзьебодисын хэмжээ нь ердөө л эзлэхүүн юм. Эцсийн эцэст, молийн тоо нь масс ба молийн массын коэффициенттэй нэгэн зэрэг тэнцүү байх болно. Менделеев-Клапейроны тэгшитгэл яг ийм харагдаж байна. Энэ нь хамгийн тохиромжтой хий ямар төрлийн систем үүсгэдэг талаар тодорхой ойлголт өгдөг. Идеал хийн төлөвийн тэгшитгэл нь дараах хэлбэртэй байна: pV=mRT/M.
Даралтын томьёог гарга
Олдсон илэрхийллүүдээрээ дахин хэдэн заль мэхийг хийцгээе. Үүнийг хийхийн тулд Менделеев-Клапейроны тэгшитгэлийн баруун талыг Авогадро тоогоор үржүүлж хуваана. Одоо бид бодисын хэмжээг Авогадро тоогоор сайтар судалж байна. Энэ нь хий дэх молекулуудын нийт тооноос өөр зүйл биш юм. Гэхдээ үүнтэй зэрэгцэн бүх нийтийн хийн тогтмолыг Авогадрогийн тоонд харьцуулсан харьцаа нь Больцманы тогтмолтай тэнцүү байх болно. Тиймээс даралтын томъёог дараах байдлаар бичиж болно: p=NkT/V эсвэл p=nkT. Энд n тэмдэг нь бөөмийн концентраци юм.
Хийн хамгийн тохиромжтой процесс
Молекулын физикт изопроцесс гэж байдаг. Эдгээр нь тогтмол параметрүүдийн аль нэгэнд системд явагддаг термодинамик процессууд юм. Энэ тохиолдолд бодисын масс нь тогтмол байх ёстой. Тэдгээрийг илүү нарийвчлан авч үзье. Тэгэхээр, идеал хийн хуулиуд.
Даралт тогтмол байна
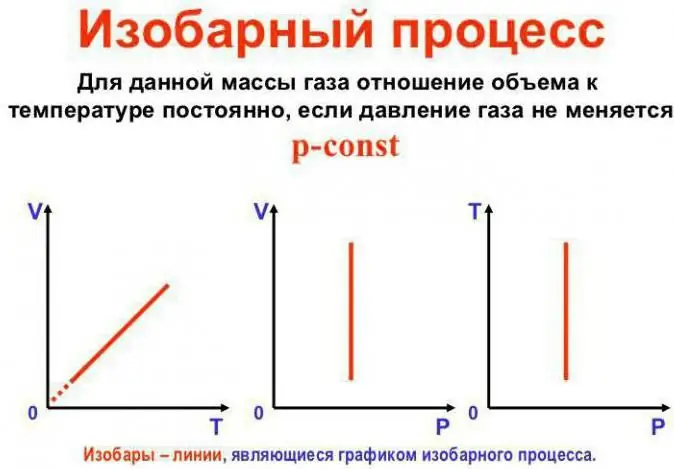
Энэ бол Гэй-Люссакийн хууль. Энэ нь иймэрхүү харагдаж байна: V/T=const. Үүнийг өөр аргаар дахин бичиж болно: V=Vo (1 + at). Энд a нь 1/273.15 K^-1-тэй тэнцүү бөгөөд "эзэлхүүний тэлэлтийн коэффициент" гэж нэрлэгддэг. Бид температурыг Цельсийн болон аль алинд нь сольж болноКелвин масштаб. Сүүлчийн тохиолдолд бид V=Voat томъёог авна.
Эзлэхүүн тогтмол байна

Энэ бол Гей-Люссакийн хоёр дахь хууль бөгөөд үүнийг ихэвчлэн Чарльзын хууль гэж нэрлэдэг. Энэ нь иймэрхүү харагдаж байна: p/T=const. Өөр нэг томъёолол байдаг: p=po (1 + at). Өмнөх жишээний дагуу өөрчлөлтийг хийж болно. Таны харж байгаагаар хамгийн тохиромжтой хийн хуулиуд заримдаа хоорондоо нэлээд төстэй байдаг.
Температур тогтмол байна

Хэрэв идеал хийн температур тогтмол байвал Бойл-Мариотын хуулийг гаргаж болно. Үүнийг ингэж бичиж болно: pV=const.
Холбогдох ойлголт 2: Хэсэгчилсэн даралт
Бидэнд хийтэй сав байна гэж бодъё. Энэ нь холимог байх болно. Систем нь дулааны тэнцвэрт байдалд байгаа бөгөөд хийнүүд нь бие биетэйгээ урвалд ордоггүй. Энд N нь нийт молекулуудын тоог илэрхийлнэ. N1, N2 гэх мэт хольцын бүрэлдэхүүн хэсэг тус бүрийн молекулын тоо. p=nkT=NkT/V даралтын томъёог авч үзье. Үүнийг тодорхой тохиолдолд нээж болно. Хоёр бүрэлдэхүүн хэсэгтэй хольцын хувьд томъёо нь дараах хэлбэртэй байна: p=(N1 + N2) kT/V. Гэхдээ дараа нь нийт даралтыг хольц бүрийн хэсэгчилсэн даралтын дүнгээс гаргаж авах болно. Тэгэхээр энэ нь p1 + p2 гэх мэт харагдах болно. Эдгээр нь хэсэгчилсэн дарамт болно.
Энэ юунд зориулагдсан бэ?
Бидний олж авсан томьёо нь систем дэх даралтыг молекулын бүлэг тус бүрээс байгааг харуулж байна. Дашрамд хэлэхэд энэ нь хамаарахгүйбусад. Далтон энэ хуулийг боловсруулахдаа үүнийг ашигласан бөгөөд хожим түүний нэрээр нэрлэсэн: хий нь хоорондоо химийн урвалд ордоггүй хольцод нийт даралт нь хэсэгчилсэн даралтын нийлбэртэй тэнцүү байх болно.






