Математикт нийлбэр (Грекийн том сигма тэмдгээр тэмдэглэгдсэн) нь тоонуудын нийлбэрүүдийн багц юм. Хэмжээ хэд вэ? Энэ бол ийм үйлдлийн үр дүн юм. Хэрэв тоонуудыг зүүнээс баруун тийш ар араас нь нэмбэл завсрын үр дүн нь хэсэгчилсэн нийлбэр болно.
Ямар дүн вэ?
Нийлгэх тоо нь бүхэл тоо, оновчтой, бодит эсвэл нийлмэл тоо байж болно. Тэдгээрээс гадна өөр төрлийн утгыг нэмж болно: вектор, матриц, олон гишүүнт, ерөнхийдөө аливаа нэмэлт бүлгийн элементүүд (эсвэл бүр моноид).
Нэр томъёоны элементүүдийн тоо хязгаартай бол нийлбэр нь үргэлж тодорхой утгыг өгдөг. Хязгааргүй утгуудын нийлбэрийг цуврал гэж нэрлэдэг. Үүний утгыг ихэвчлэн хязгаар ашиглан тодорхойлж болно (хэдийгээр заримдаа утга нь хязгааргүй байж болно).
Дараалал
[3, 7, 2, 1] тоонуудын нийлбэрийг утга нь түүнд орсон цифрүүдийн нийлбэр болох илэрхийллээр тодорхойлж болно, жишээ нь 3 + 7 + 2 + 1=13. нэмэлтассоциатив байдлаар, нийлбэр нь нэр томъёог хэрхэн бүлэглэхээс хамаардаггүй, жишээлбэл, (3 + 7) + (2 + 1) ба 3 + ((7 + 2) + 1) хоёулаа есөнтэй тэнцэх тул хаалтанд ихэвчлэн өгөгддөг.. Нэмэх нь мөн солигддог тул нэр томъёог өөрчлөх нь нийлбэрийн утгыг өөрчлөхгүй. Энэ өмч хязгааргүй нийлбэрт ажиллахгүй байж болохыг анхаарна уу.

Ийм төрлийн дарааллыг нэгтгэх тусгай тэмдэглэгээ байхгүй. Хоёроос бага элемент байвал бага зэрэг нюанс бий. Нэг гишүүний дарааллын нийлбэр нь нэмэх тэмдэг агуулаагүй (энэ нь тухайн тооны хэлбэрээс ялгагдахгүй) бөгөөд хэрэв ямар ч элемент байхгүй бол үүнийг бичих ч боломжгүй (гэхдээ оронд нь үүнийг тэмдэглэж болно). түүний утга "0"). Гэсэн хэдий ч, дарааллын нөхцөлийг функц гэх мэт тодорхой загвараар тодорхойлсон бол нийлбэрийн оператор нь ашигтай эсвэл бүр чухал байж болно.
Бичлэг
Нийлбэр гэж юу болохыг ойлгохын тулд гадаад төрхийг нь шинжлэх шаардлагатай.
1-ээс 100 хүртэлх бүхэл тоонуудын дарааллыг нийлбэрлэхдээ дутуу гишүүдийг заах зуйван агуулсан илэрхийллийг ихэвчлэн ашигладаг: 1 + 2 + 3 + 4 + … + 99 + 100. Загвар нь: Энэ жишээнээс харахад маш амархан. Гэсэн хэдий ч илүү төвөгтэй сонголтуудын хувьд "Σ" нийлбэрийн операторын тусламжтайгаар хүрч болох элементүүдийн утгыг олоход ашигладаг дүрмийг яг таг зааж өгөх шаардлагатай. Энэ тэмдгийг (сигма) ашиглан та дараах тэмдэглэгээг хэрэглэж болно:
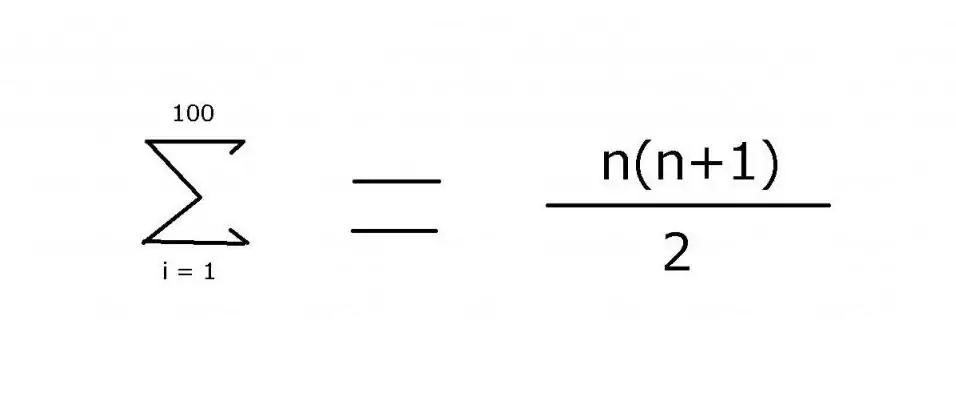
Энэ илэрхийллийн утга нь 5050. Үүнийг томъёоны хоёр дахь хэсэг үүссэн математик индукцийг ашиглан олж болно.
Өөр өөр дарааллын хувьд томъёо өөрчлөгдөнө. Бичлэг хийх үйл явц нь хязгааргүй дарааллын өмнөх зургийг хайж, дараа нь томьёогоор дүрслэх хүртэл багасдаг. Үүнийг хийснээр тодорхой тохиолдолд ямар дүн байгааг ойлгоход хэцүү биш юм.
Тоонуудыг тэмдэгтүүдтэй нь (нэмэх, хасах) нэмдэг гэдгийг тодруулах шаардлагатай үед алгебрийн нийлбэр гэсэн нэр томъёог ашиглана. Жишээлбэл, цахилгаан хэлхээний онолд Кирхгофын хэлхээний хуулиуд нь зангилааны дотогш болон гадагш урсах гүйдлийн эсрэг шинж тэмдэг өгдөг дамжуулагчийн сүлжээн дэх гүйдлийн алгебрийн нийлбэрийг авч үздэг.






