Термодинамикийн чухал хэсэг нь бодисын янз бүрийн үе хоорондын хувирлыг судлах явдал юм, учир нь эдгээр үйл явц нь практикт тохиолддог бөгөөд тодорхой нөхцөлд системийн үйл ажиллагааг урьдчилан таамаглахад чухал ач холбогдолтой юм. Эдгээр хувиргалтыг фазын шилжилт гэж нэрлэдэг бөгөөд үүнд нийтлэл зориулагдсан болно.
Үе шат ба системийн бүрэлдэхүүн хэсгийн тухай ойлголт

Физикт фазын шилжилтийг авч үзэхийн өмнө фазын тухай ойлголтыг тодорхойлох шаардлагатай. Ерөнхий физикийн хичээлээс мэдэгдэж байгаагаар бодис нь хий, хатуу, шингэн гэсэн гурван төлөвтэй байдаг. Шинжлэх ухааны тусгай хэсэгт - термодинамикийн хувьд хуулиудыг нэгтгэх төлөвт бус харин материйн үе шатуудад зориулж томъёолдог. Фаз гэдэг нь нэг төрлийн бүтэцтэй, тодорхой физик, химийн шинж чанараараа тодорхойлогддог, бусад матераас хил хязгаараар тусгаарлагдсан материйн тодорхой эзэлхүүнийг ойлгодог бөгөөд үүнийг интерфаз гэж нэрлэдэг.
Тиймээс "үе шат" гэсэн ойлголт нь шинж чанаруудын талаар илүү практик ач холбогдолтой мэдээллийг агуулдаг.түүний нэгдмэл байдлын байдлаас илүү. Жишээлбэл, төмөр зэрэг металлын хатуу төлөв нь дараах үе шатуудад байж болно: бага температурт соронзон биет төвтэй куб (BCC), бага температурт соронзон бус bcc, нүүр төвтэй куб (fcc), өндөр- температур соронзон бус Bcc.
Термодинамикийн хуулиудад "фаз" гэсэн ойлголтоос гадна "бүрэлдэхүүн" гэсэн нэр томъёог ашигладаг бөгөөд энэ нь тодорхой системийг бүрдүүлдэг химийн элементүүдийн тоог илэрхийлдэг. Энэ нь фаз нь нэг бүрэлдэхүүн хэсэг (1 химийн элемент) эсвэл олон бүрэлдэхүүн хэсэг (хэд хэдэн химийн элемент) байж болно гэсэн үг юм.
Гиббсийн теорем ба системийн фаз хоорондын тэнцвэр

Фазын шилжилтийг ойлгохын тулд тэдгээрийн хоорондын тэнцвэрийн нөхцлийг мэдэх шаардлагатай. Гадны нөлөөллөөс тусгаарлагдсан системийн нийт Гиббсийн энерги өөрчлөгдөхөө болих үед тэнцвэрийн төлөвт хүрнэ гэж үзвэл Гиббсын тэгшитгэлийн системийг тус бүрээр нь шийдэж эдгээр нөхцлүүдийг математикийн аргаар гаргаж болно.
Заасан тэгшитгэлийн системийг шийдсэний үр дүнд хэд хэдэн фазын хооронд тэнцвэрт байдал бий болох нөхцөлүүд гарч ирдэг: бүх үе шат дахь даралт, химийн потенциал, температурын үед л тусгаарлагдсан систем үүсэхээ болино. хоорондоо тэнцүү байна.
Тэнцвэрийн Гиббсийн фазын дүрэм

Хэд хэдэн үе шат, бүрэлдэхүүн хэсгүүдээс бүрдсэн систем нь зөвхөн тэнцвэрт байдалд байж чаддаггүйтодорхой нөхцөлд, жишээлбэл, тодорхой температур, даралтаар. Тэнцвэрийн Гиббсийн теоремын зарим хувьсагчийг энэ тэнцвэрт байгаа фазын тоо болон бүрэлдэхүүн хэсгүүдийн тоог хоёуланг нь хадгалахын зэрэгцээ өөрчилж болно. Системийн тэнцвэрт байдлыг алдагдуулахгүйгээр өөрчлөх боломжтой хувьсагчдын тоог энэ системийн эрх чөлөөний тоо гэнэ.
f фаз ба k бүрэлдэхүүн хэсгүүдээс бүрдэх системийн l эрх чөлөөний тоог Гиббсын фазын дүрмээр өвөрмөц байдлаар тодорхойлно. Энэ дүрмийг математикийн хувьд дараах байдлаар бичнэ: l + f=k + 2. Энэ дүрэмтэй хэрхэн ажиллах вэ? Маш энгийн. Жишээлбэл, систем нь f=3 тэнцвэрийн үе шатуудаас бүрддэг нь мэдэгдэж байна. Ийм системд хамгийн бага хэдэн бүрэлдэхүүн хэсэг байж болох вэ? Асуултанд дараахь үндэслэлээр хариулж болно: тэнцвэрт байдлын хувьд хамгийн хатуу нөхцөл нь зөвхөн тодорхой үзүүлэлтүүд дээр хэрэгждэг, өөрөөр хэлбэл термодинамикийн аливаа параметрийн өөрчлөлт нь тэнцвэргүй байдалд хүргэдэг. Энэ нь эрх чөлөөний тоо l=0 гэсэн үг. l ба f-ийн мэдэгдэж буй утгуудыг орлуулснаар бид k=1-ийг олж авна, өөрөөр хэлбэл гурван фаз тэнцвэрт байдалд байгаа систем нь нэг бүрэлдэхүүн хэсгээс бүрдэж болно. Үүний тод жишээ нь усны гурвалсан цэг бөгөөд мөс, шингэн ус, уур нь тодорхой температур, даралтад тэнцвэрт байдалд оршдог.
Фазын хувиргалтуудын ангилал
Хэрэв та тэнцвэрт байдалд байгаа системийн зарим термодинамик параметрүүдийг өөрчилж эхэлбэл нэг фаз хэрхэн алга болж нөгөө фаз гарч ирэхийг ажиглаж болно. Энэ үйл явцын энгийн жишээ бол мөсийг халах үед хайлах явдал юм.
Гиббсын тэгшитгэл нь зөвхөн хоёр хувьсагчаас (даралт ба температур) хамаардаг ба фазын шилжилт нь эдгээр хувьсагчийн өөрчлөлтийг агуулдаг тул математикийн хувьд Гиббсын энергийг түүнийхтэй харьцуулан ялгах замаар үе шат хоорондын шилжилтийг тодорхойлж болно. хувьсагч. Чухам ийм аргыг Австрийн физикч Пол Эренфест 1933 онд фазын тэнцвэрт байдал өөрчлөгдөхөд тохиолддог бүх мэдэгдэж буй термодинамик процессуудын ангиллыг эмхэтгэхдээ ашигласан.
Термодинамикийн үндсээс үзэхэд Гиббсийн энергийн температурын анхны дериватив нь системийн энтропийн өөрчлөлттэй тэнцүү байна. Даралттай холбоотой Гиббсийн энергийн дериватив нь эзэлхүүний өөрчлөлттэй тэнцүү байна. Хэрэв систем дэх фазууд өөрчлөгдөхөд энтропи эсвэл эзэлхүүн нь тасалдвал, өөрөөр хэлбэл тэдгээр нь огцом өөрчлөгдвөл эхний эрэмбийн фазын шилжилтийн тухай ярьдаг.
Цаашилбал, Гиббсийн энергийн температур ба даралттай холбоотой хоёр дахь дериватив нь дулаан багтаамж ба эзэлхүүний тэлэлтийн коэффициент юм. Хэрэв үе шат хоорондын өөрчлөлт нь заасан физик хэмжигдэхүүний утгуудын тасалдал дагалддаг бол хоёр дахь дарааллын фазын шилжилтийн тухай ярьж байна.
Үе шат хоорондын өөрчлөлтийн жишээ

Байгаль дээр асар олон тооны өөр өөр шилжилтүүд байдаг. Энэ ангиллын хүрээнд эхний төрлийн шилжилтийн тод жишээ бол системд эзлэхүүн үсрэх үед метал хайлуулах процесс эсвэл агаараас усны уурыг конденсацлах үйл явц юм.
Хэрэв бид хоёр дахь эрэмбийн шилжилтийн тухай ярих юм бол гайхалтай жишээ бол төмрийг температурт соронзон байдлаас парамагнит төлөвт хувиргах явдал юм.768 ºC буюу үнэмлэхүй тэгтэй ойролцоо температурт металл дамжуулагчийг хэт дамжуулагч төлөвт шилжүүлэх.
Эхний төрлийн шилжилтийг дүрсэлсэн тэгшитгэлүүд
Практикт системд фазын хувирал үүсэх үед температур, даралт, шингэсэн (суллагдсан) энерги хэрхэн өөрчлөгддөгийг мэдэх шаардлагатай байдаг. Энэ зорилгоор хоёр чухал тэгшитгэлийг ашигладаг. Тэдгээрийг термодинамикийн үндсүүдийн мэдлэг дээр үндэслэн олж авдаг:
- Янз бүрийн фазын хооронд хувирах үед даралт ба температурын хамаарлыг тогтоодог Клапейроны томьёо.
- Хувиргах явцад шингэсэн (суллагдсан) энерги болон системийн температурыг холбодог Клаузиусын томъёо.
Тэгшитгэлийг хоёуланг нь ашиглах нь физик хэмжигдэхүүний тоон хамаарлыг олж авахад төдийгүй фазын диаграмм дээрх тэнцвэрийн муруйн налуугийн тэмдгийг тодорхойлоход оршино.
Хоёр дахь төрлийн шилжилтийг тайлбарлах тэгшитгэл

1-р ба 2-р төрлийн фазын шилжилтийг өөр өөр тэгшитгэлээр тайлбарладаг, учир нь Клаузиус ба Клаузиус тэгшитгэлийг хоёрдугаар эрэмбийн шилжилтэд хэрэглэх нь математикийн тодорхойгүй байдалд хүргэдэг.
Сүүлийн зүйлийг тайлбарлахын тулд хувиргалт хийх явцад дулааны багтаамж, эзэлхүүний тэлэлтийн коэффициентийн өөрчлөлтийн талаарх мэдлэгээр дамжуулан даралт ба температурын өөрчлөлтийн хоорондын хамаарлыг тогтоодог Эренфестийн тэгшитгэлийг ашигладаг. Эренфестийн тэгшитгэлийг соронзон орон байхгүй үед дамжуулагч ба хэт дамжуулагчийн шилжилтийг тодорхойлоход ашигладаг.
Ач холбогдолфазын диаграмм
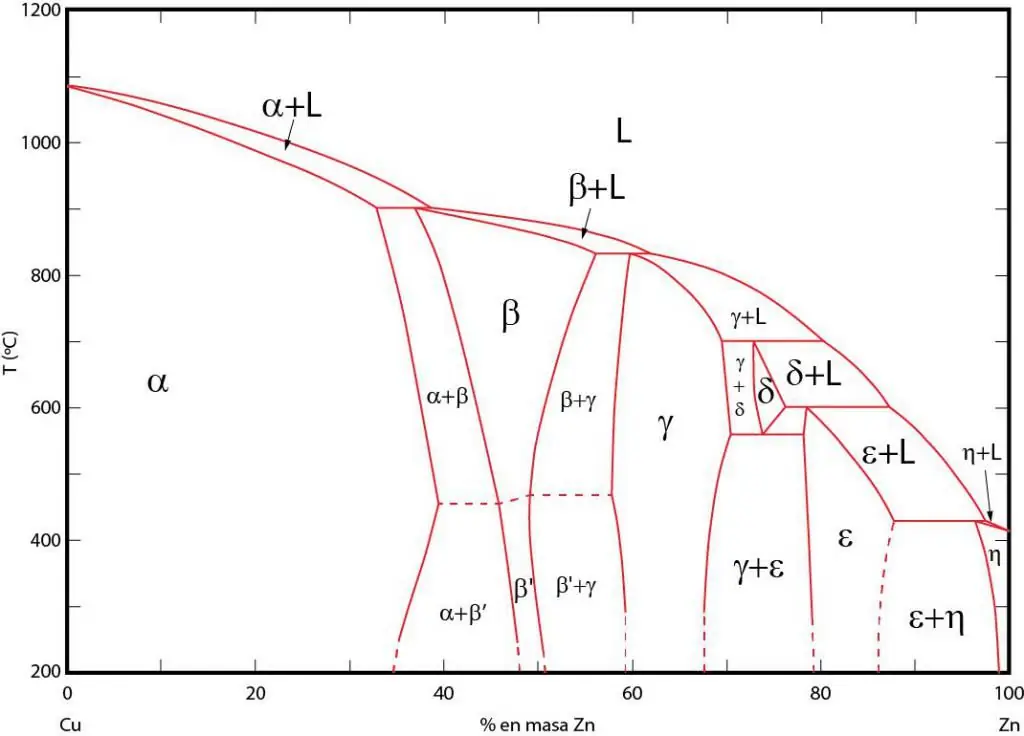
Үе шатын диаграмм нь тэнцвэрт байдалд байгаа харгалзах фазуудын график дүрслэл юм. Эдгээр талбайнууд нь үе шатуудын хоорондох тэнцвэрийн шугамаар тусгаарлагддаг. P-T (даралт-температур), T-V (температур-эзэлхүүн), P-V (даралт-эзэлхүүн) фазын диаграммыг ихэвчлэн ашигладаг.
Фазын диаграмын ач холбогдол нь гадаад нөхцөл байдал зохих ёсоор өөрчлөгдөх үед систем ямар үе шатанд байхыг урьдчилан таамаглах боломжийг олгодогт оршино. Энэ мэдээллийг хүссэн шинж чанартай бүтэцтэй болгохын тулд янз бүрийн материалыг дулааны боловсруулалтанд ашигладаг.






