Титиус-Бодегийн дүрэм (заримдаа Бодегийн хууль гэж нэрлэдэг) нь нар зэрэг тойрог замын зарим систем дэх биеүүд гаригийн дарааллаас хамааран хагас тэнхлэгийн дагуу эргэдэг гэсэн таамаглал юм. Энэ томьёо нь гадагшаа тэлвэл гараг бүр өмнөхөөсөө нарнаас хоёр дахин хол байх болно гэдгийг харуулж байна.
Таамаглал нь Церера (астероидын бүсэд) болон Тэнгэрийн ван гаригийн тойрог замыг зөв таамагласан боловч Далай вангийн тойрог замыг тодорхойлж чадаагүй бөгөөд эцэст нь нарны аймаг үүсэх онолоор солигдсон. Энэ нь Иоганн Даниел Титиус, Иоганн Элерт Боде нарын нэрээр нэрлэгдсэн.

Origins
Бодегийн хуулийг ойртуулсан цувралын тухай анхны дурдлагыг 1715 онд хэвлэгдсэн Дэвид Грегоригийн Одон орон судлалын элементүүдээс олж болно. Үүнд: “… Нарнаас Дэлхий хүртэлх зайг арван тэнцүү хэсэгт хуваасан гэж үзвэл Мөнгөн ус дөрөв орчим, Сугараас долоо, Ангараг гарагаас арван тав, Бархасбадьаас тавин хоёр байх болно., мөн Санчир гаригаас ерэн тав . Үүнтэй төстэй санал, магадгүй Грегоригийн санаанаас санаа авсан байж магадгүй, Кристиан Вольфын 1724 онд хэвлэгдсэн бүтээлд гардаг.
1764 онд Чарльз Боннет "Байгалийн тухай эргэцүүлэл" номондоо: "Бид нарны аймгийнхаа арван долоон гарагийг [өөрөөр хэлбэл, үндсэн гаригууд болон тэдгээрийн дагуулуудыг] мэддэг ч бид үүнийг сайн мэдэхгүй байна. Тэд байхгүй болсон." Үүний тулд 1766 онд Боннетийн бүтээлийг орчуулсан Иоганн Даниел Титиус 7-р хуудасны доод талд, 8-р хуудасны дээд талд өөрийн гэсэн хоёр догол мөр нэмж оруулсан байна. Боннетийн эх бичвэрт шинэ интерполяцлагдсан догол мөр олдоогүй: Итали хэл дээр ч байхгүй. бүтээлийн англи орчуулга ч биш.
Титиусын нээлт
Титиусын харилцан уялдаатай бичвэрт хоёр хэсэг бий. Эхнийх нь нарнаас гарагуудын зайны дарааллыг тайлбарладаг. Энэ нь мөн нарнаас Бархасбадь хүртэлх зайны талаар хэдэн үг агуулдаг. Гэхдээ энэ бол текстийн төгсгөл биш.
Титиус-Бодегийн дүрмийн томъёоны талаар хэдэн үг хэлэх нь зүйтэй болов уу. Гаригуудын хоорондох зайд анхаарлаа хандуулж, бараг бүгдээрээ бие биенийнхээ хэмжээтэй тохирч байгаа хувь хэмжээгээр бие биенээсээ тусгаарлагдсан болохыг олж мэдээрэй. Нарнаас Санчир гариг хүртэлх зайг 100 хэсэгт хуваах; Дараа нь Мөнгөн ус нарнаас ийм дөрвөн хэсгээс тусгаарлагддаг; Сугар - 4 + 3=7 ийм хэсгүүдэд; Дэлхий - 4+6=10-аар; Ангараг - 4+12=16.
Гэхдээ Ангараг гарагаас Бархасбадь хүртэл ийм нарийн явцаас хазайлт байгааг анхаарна уу. Ангараг гарагаас 4+24=28 ийм хэсгүүдийн орон зай гарч ирдэг боловч одоогоор тэнд нэг ч гариг нээгдээгүй байна. Гэхдээ лорд архитектор энэ газрыг хоосон орхих ёстой юу? Хэзээ ч үгүй. ТэгэхээрЭнэ орон зай нь Ангараг гарагийн хараахан нээгдээгүй дагуулуудад хамаарах нь эргэлзээгүй гэж бодъё, мөн Бархасбадь гаригийн эргэн тойронд ямар ч дуран хараахан хараахан хараахан хараахан амжаагүй хэд хэдэн жижиг дагуулууд байсаар байгааг нэмье.

Rise of the Bode
1772 онд Иоганн Элерт Боде хорин таван настайдаа Anleitung zur Kenntniss des gestirnten Himmels ("Одтой тэнгэрийн тухай мэдлэгийн хөтөч") хэмээх одон орны эмхэтгэлийнхээ хоёр дахь хэвлэлийг бичиж дуусгажээ. Дараах зүүлт тайлбарыг нэмж, эх сурвалжгүй боловч дараагийн хувилбаруудад тэмдэглэсэн. Бодегийн дурсамжаас Титиусын эрх мэдлийг илт хүлээн зөвшөөрсөн ишлэлийг олж болно.

Үзэл бодол
Сүүлийн танилцуулгад Титиус-Бодегийн дүрэм ингэж сонсогддог: хэрвээ Нарнаас Санчир гариг хүртэлх зайг 100-тай тэнцүү авбал Мөнгөн ус нарнаас ийм дөрвөн хэсэгт хуваагдана. Сугар - 4+3=7. Дэлхий - 4+6=10. Ангараг - 4+12=16.
Одоо энэ эрэмбэлэгдсэн ахиц дэвшилд цоорхой байна. Ангараг гарагийн дараа 4+24=28 гэсэн тооцоотой орон зай гарч ирэх бөгөөд тэнд нэг ч гариг хараахан үзээгүй байна. Орчлон ертөнцийг үүсгэн байгуулагч энэ орон зайг хоосон орхисон гэвэл бид итгэх үү? Мэдээж үгүй. Эндээс бид 4+48=52 тооцооны хэлбэрээр Бархасбадийн зайд хүрч, эцэст нь Санчир гаригийн зайд - 4+96=100 байна.

Бүх тодорхой төрлийн болон тойрог замын радиустай холбоотой эдгээр хоёр мэдэгдэл нь эртний үеэс ирсэн бололтой.одон орон судлал. Эдгээр онолын ихэнх нь XVII зуунаас өмнөх үетэй холбоотой.
Нөлөө
Титиус бол Германы гүн ухаантан Кристиан Фрейхер фон Вольфын (1679-1754) шавь юм. Боннетийн бүтээлд оруулсан текстийн хоёр дахь хэсэг нь фон Вольфын 1723 онд хэвлэгдсэн Vernunftige Gedanken von den Wirkungen der Natur бүтээлээс сэдэвлэсэн болно.
20-р зууны уран зохиолд Титиус-Бодегийн дүрмийн зохиогчийн эрхийг Германы гүн ухаантанд даатгадаг. Хэрэв тийм бол Титиус түүнээс суралцаж чадна. Өөр нэг эртний лавлагааг Жеймс Грегори 1702 онд Astronomiae Physicae et geometryae Elementa номдоо бичсэн бөгөөд гаригийн зайн 4, 7, 10, 16, 52, 100-ын дараалал нь 2 харьцааны геометр прогресс болсон.
Энэ бол Ньютоны хамгийн ойр томьёо бөгөөд Боннетийн ном Германд хэвлэгдэхээс хэдэн жилийн өмнө Бенжамин Мартин, Томас Сиард нарын зохиолуудаас бас олдсон.
Цаашдын ажил ба практик үр дагавар
Титиус, Боде нар уг хууль шинэ гаригуудыг нээхэд хүргэнэ гэж найдаж байсан бөгөөд үнэхээр Тэнгэрийн ван, Церера хоёрыг нээсэн нь хуульд нийцсэн зай нь түүнийг шинжлэх ухааны ертөнцөд хүлээн зөвшөөрөхөд нөлөөлсөн.
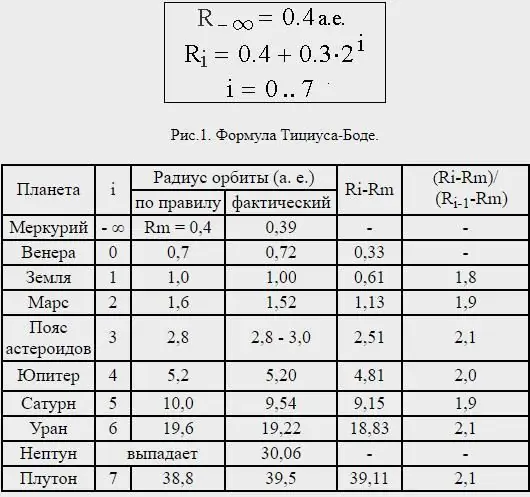
Гэсэн хэдий ч Далай вангийн зай маш зөрүүтэй байсан ба үнэндээ Плутон одоо гариг гэж тооцогдохгүй байгаа нь Тэнгэрийн ван гарагаас бусад гаригийн хувьд таамагласан Титиус-Бодегийн хуультай ойролцоо зайд байгаа юм.
Анх нийтлэгдсэн хуулийг Буд болон Санчир гаригийн бүх мэдэгдэж буй гаригууд ойролцоогоор хангасан бөгөөд тэдгээрийн хоорондох зай завсар байна.дөрөв ба тав дахь гаригууд. Энэ нь 1781 онд Тэнгэрийн ван гарагийг нээх хүртэл сонирхолтой боловч тийм ч чухал биш тоо гэж тооцогддог байсан бөгөөд энэ нь цувралд багтах болно.
Энэ нээлт дээр үндэслэн Боде тав дахь гаригийг хайхыг уриалав. Астероидын бүс дэх хамгийн том биет болох Церес 1801 онд Бодегийн таамагласан байрлалаас олдсон. 1846 онд Далай ван нээгдэх хүртэл Бодегийн хуулийг нийтээр хүлээн зөвшөөрч, хуультай зөрчилдөж байсан.
Үүний зэрэгцээ бүсээс олдсон олон тооны астероидууд Сересийг гаригуудын жагсаалтаас хасав. Бодегийн хуулийг одон орон судлаач, логикч Чарльз Сандерс Пирс 1898 онд буруу үндэслэлийн жишээ болгон авч хэлэлцсэн.

Асуудлыг боловсруулах
1930 онд Плутоныг нээсэн нь асуудлыг улам хүндрүүлсэн. Хэдийгээр энэ нь Бодегийн хуулиар таамагласан байр суурьтай таарахгүй байсан ч энэ нь Далай вангийн хувьд хуулиас урьдчилан таамагласан байр суурьтай холбоотой байв. Гэвч дараа нь Куйперийн бүс, ялангуяа Плутоноос илүү масстай ч Бодегийн хуульд үл нийцэх Эрис биетийг нээсэн нь томьёог улам гутаасан.
Сэрдагийн оруулсан хувь нэмэр
Иезуит Томас Серда 1760 онд Барселоны Сант Жауме де Корделлийн коллежийн (Корделлийн язгууртнуудын эзэн хааны болон хааны семинар) Хааны Математикийн тэнхимд алдарт одон орон судлалын курс заажээ. Сердасын Тратадод Кеплерийн 3-р хуулийг хэрэглэснээр 10-3 нарийвчлалтайгаар олж авсан гаригуудын зай гарч ирдэг.
Хэрэв бид дэлхийгээс хол зайг 10-аар авч үзвэл бабүхэл тоо хүртэл дугуйлах, геометр прогресс [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, n=2-оос n=8 хүртэл, илэрхийлж болно. Кеплерийн аномали руу чиглэсэн дугуй жигд зохиомол хөдөлгөөнийг ашиглан гариг бүрийн харьцаатай харгалзах Rn утгыг rn=(Rn - R1) / (Rn-1 - R1) гэж авч болно, үр дүнд нь 1.82; 1, 84; 1, 86; 1.88 ба 1.90, энд rn=2 - 0.02 (12 - n) нь Кеплерийн тасралтгүй байдал болон Титиус-Боде хуулийн хоорондох тодорхой хамаарал бөгөөд үүнийг санамсаргүй тооны давхцал гэж үздэг. Тооцооллын үр дүн хоёр дөхөж байгаа ч 1-ийн 82 тоог дугуйрсан гэж үзэж болно.

Гариг n=1-ээс n=8 хүртэлх дундаж хурд нь нарнаас хол зайг багасгаж, n=7 (тойрог тойргийн резонанс) -аас сэргэхийн тулд n=2 дахь жигд бууралтаас ялгаатай. Энэ нь нарнаас Бархасбадь хүртэлх зайд нөлөөлдөг. Гэсэн хэдий ч өгүүлэлд зориулагдсан алдартай дүрмийн хүрээнд бусад бүх объектын хоорондох зайг мөн энэ математик динамикаар тодорхойлдог.
Онолын тал
Титиус-Бодегийн дүрмийн үндсэн онолын баттай тайлбар байхгүй ч тойрог замын резонансын болон эрх чөлөөний зэрэггүй байдлын хослолыг харгалзан үзвэл аливаа тогтвортой гаригийн систем нь дээр дурдсан загварыг давтах магадлал өндөртэй байж магадгүй юм. Энэ онолыг хоёр эрдэмтэн гаргасан.
Энэ нь "байгалийн хууль" биш математикийн давхцал байж болох тул заримдаа үүнийг "хууль" гэхээсээ илүү дүрэм гэж нэрлэдэг. Гэсэн хэдий ч астрофизикч Алан Босс үүнийг энгийн зүйл гэж баталж байнасанамсаргүй тохиолдлын улмаас гаригийн шинжлэх ухааны Icarus сэтгүүл "хуулийн" сайжруулсан хувилбарыг гаргахыг оролдсон нийтлэлийг цаашид хүлээн авахаа больсон.
Орбитал резонанс
Тойрог эргэдэг томоохон биетүүдийн тойрог замын резонансын нөлөөгөөр Нарны эргэн тойронд урт хугацааны тогтвортой тойрог замгүй бүсүүд үүсдэг. Гариг үүсэх симуляцийн үр дүн нь санамсаргүй байдлаар сонгосон тогтвортой гаригийн систем нь Титиус-Бодегийн дүрмийг хангах магадлалтай гэсэн санааг баталж байна.

Дубрулле ба Гранер
Дубрулле, Гранер нар эрчим хүчний хуулийн зайны дүрэм нь эргэлтийн өөрчлөгдөөгүй (үүл ба түүний агуулга нь тэнхлэгийн тэгш хэмтэй байдаг) болон масштабын өөрчлөгддөггүй байдал (үүл ба түүний агуулга) гэсэн хоёр тэгш хэмтэй гаригийн системийн үүл нурах загваруудын үр дагавар байж болохыг харуулсан. түүний агуулга бүх хэмжүүр дээр адилхан харагдаж байна).
Сүүлийнх нь үймээн самуун зэрэг гараг үүсэхэд чухал үүрэг гүйцэтгэдэг гэж үздэг олон үзэгдлийн онцлог юм. Титиус, Боде нарын санал болгосон нарнаас нарны аймгийн гараг хүртэлх зайг Дубрул, Гранер нарын судалгааны хүрээнд засаагүй болно.






